Validating SSU taxonomy classifiers is a challenging problem.
1. Classifiers use different taxonomies which cannot be directly compared, e.g. NCBI, SILVA, Greengenes, RDP, Bergey.
2. It is not clear how to obtain "gold standard" data where query sequences have reliably known taxonomies.
3. Classifiers vary in the methods they use for reporting confidence in the prediction. GAST does not provide any confidence score. The RDP Naive Bayesian Classifier (RDPC) reports a bootstrap confidence score which unfortunately does not function as a true P-value. UTAX reports a true P-value. How can such methods be fairly compared?
Given these problems it appears to be impossible to validate classifiers as they are used "in the wild", i.e. by using their web sites or stand-alone tools with their standard training/reference data . However, it is possible to measure the relative performance of different classification algorithms by dividing a gold standard reference set into training and test sets.
A gold standard set can be obtained by selecting a conservative subset of known SSU sequences such as finished genomes and isolate sequences.
If we divide this set into two roughly equal halves (training set and test set), then we can make a fair assessment of the relative performance of different classification algorithms.
The absolute performance cannot be measured because it will be highly dependent on the composition of the community (human gut vs. soil vs. buried Antarctic lake) and how well represented the community is in the full training data.
Classification is easy at high identity
If the query sequence matches a reference sequence with high identity, then
it probably has the same taxonomy, except perhaps at the lowest levels (say,
species or strain). All
classifiers are based in some way on sequence identity, and all will give good
results when there is high identity. The real challenge for a classifier is how
to handle sequences with lower identity. For example, suppose you have a 88%
match to a 16S sequence. Should it be assigned to the same genus, family or
order? How can we measure the accuracy of a classifier when presented with this
type of challenge?
The RDP Classifier "leave-one-out" method
The RDP Naive Bayesian Classifier paper uses
leave-one-out. which works as follows. They take their training database (D) and
remove one sequence (call it Q) leaving a reduced database D'. They re-train
their classifier using D' and test whether Q is correctly classified. They
repeat this for all sequences in the database and average. Each level is tested (genus, family...)
to measure sensitivity and error rate.
The RDP validation method grossly over-states accuracy
The RDP leave-one-out method is highly
misleading. RDPC classifies to genus level (not to species), and the average number of reference sequences per genus in their training
set is five, so doing leave-one-out effectively asks the question "how well can
you classify a novel sequence if four other members of the genus are present in
the reference database". This is might be reasonable for genus-level
classification if you are attempting to classify a well-studied environment
(say, human gut) where you believe that most genera are present in your training
set. But it does not test how well the classifier performs when challenged with
novel genera.
Also, the RDP paper uses zero as the bootstrap confidence cutoff for reporting accuracy. Yes, zero! So "accuracy" is really sensitivity when sensitivity is the maximum possible. In practice, a cutoff of 50% is typically used for short NGS tags. With this cutoff, sensitivity will be much lower.
At higher levels, this approach is just nonsense. The RDP papers claims e.g. 98% sensitivity at family level, but that's simply not informative when the genus is still present for 8095 / 8978 = 90% of the sequences after deleting the test sequence.
Another way to see this is to look at the %id distribution of the nearest neighbor in their training database. 71% of the nearest neighbors have identity >=97% and 91% of nearest neighbor's have identity >=94%. If the nearest sequence in the reference database is within 97% or 94%, classification is easy. Any sane classifier should do well on this test.
This is important for data like soil, where there will be lots of novel genera. What happens when the genus is NOT present in the training data? The RDP validation method does not answer this question.
How to measure classification accuracy
What we should care about to understand
classification accuracy at higher levels is how well the classifier performs at
lower identities when it has to climb the tree. Let's say we want to measure
family level accuracy. If the genus is present, it's too easy and that's not
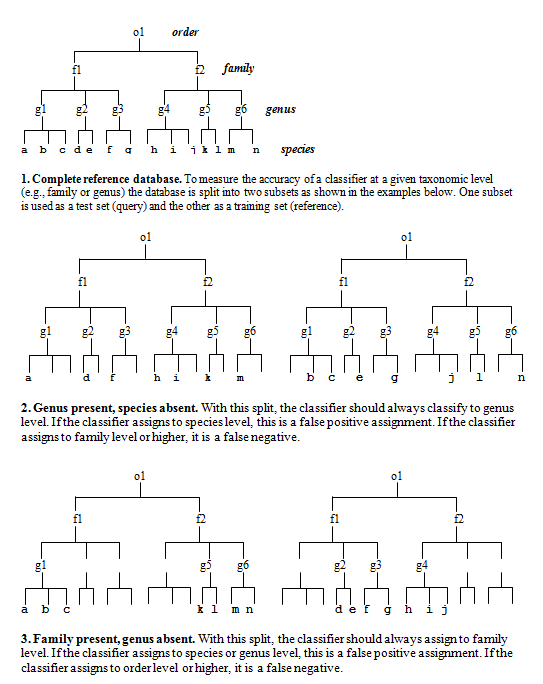
what we're trying test. I use the following method (see figure at bottom of
this page)..
Split the reference sequences into a query set (Q) and database set (D) so that all families in Q are present in D, but the same genus is never present in both. (Singleton families must be discarded). To get a correct prediction with this data, the classifier must identify the family by matching to a different genus in the same family. Since the family is always present in D, we can use this to measure family-level sensitivity: it's the fraction of Q sequences that are successfully assigned to the correct family.
This test will give some errors, but we're still going too easy on the classifier. We also want to know the error rate at family level when the family is NOT present. To do this, we split the database differently so that the same family is never present, but the level above (order, in this case) is always present. We want the order present so that there are sequences which are as close as possible without being in the same family. This is the hardest case for a classifier to deal with. Now we're asking how often does the classifier reports family when it should be reporting order.
So this is my validation protocol: For each taxonomic level (genus, family... phylum), make two Query-Database pairs by splitting your trusted reference set. In one pair (the "possible" pair), at least one example is present in the database so the classification is possible. This measures sensitivity and the error rate of misclassifying to a different taxon. The second Q-D pair ("impossible") has no examples of the taxon, so assignments at the given level are always errors. This measures the rate of "overclassification" errors.
Validating confidence scores and P-values
Informatics prediction algorithms should give a
score or P-value that indicates confidence that the prediction is correct. A
score allows the user to set a cutoff to achieve a trade-off between sensitivity
and error rate. A P-value is an estimate of the probability that the
classification is correct. Reporting a P-value is ideal, because this allows the
user to estimate the error rate for a given cutoff. If a P-value cannot be
calculated, then a confidence score is the next best thing because this still
allows the user to set a cutoff. However, with a score, the user cannot estimate
the error rate at a given cutoff and this means that error analysis for
downstream analysis is difficult or impossible.
UTAX gives a true P-value for each level (genus, family...) of each classification, i.e. an estimated probability that the classification is correct. The accuracy of the P-value can be validated by comparing the measured error rate with the predicted error rate at different cutoffs.
RDPC gives a bootstrap confidence value. The bootstrap value is not a P-value, i.e. it does not directly predict the error rate, but it does serve as a score which can be used to set of cutoff, which you cannot do with some alternatives such as GAST or "BLAST-top-hit".
We can compare the effectiveness of different classifiers and the predictive value of their P-values or confidence scores from different programs by making a graph which plots sensitivity against error rate. (For this analysis, a P-value is treated as a confidence score without asking whether the error rate it predicts is correct). If the plot shows that classifier A always has higher sensitivity at a given error rate than classifier B, then we are justified in saying that classifier A is better than classifier B. Sometimes, the curves intersect, in which case the claim is not so clear. However, in my experience, this rarely happens in the range of error rates that would be useful in practice -- with, say, an error rate of <5%, then it is usually possible to say that one classifier is definitively better than another.